En el anterior artículo de Bembibre Digital, hablé del Número de Avogadro señalando que un modo de estimar o al menos intuir los conocimientos de química de una persona es evaluar su grado de conocimiento de este célebre número. Pues bien, similar función desempeña en el caso de las matemáticas el Teorema de Pitágoras. Como es de dominio (casi) público hoy día, este teorema dice que la suma del cuadrado de los catetos de un triángulo rectángulo es igual al cuadrado de su hipotenusa. Los catetos de un triángulo rectángulo son los dos lados que forman “la escuadra”, es decir el ángulo recto y la hipotenusa el otro. La suma de los tres ángulos de un triángulo es siempre 180º es decir dos ángulos rectos (en “escuadra”) y en consecuencia si uno de los ángulos del triángulo tiene 90º es imposible que algunos de los otros dos llegue a tener 90º.Han de ser siempre menores.
En la Red he leído que el Teorema de Pitágoras es el que cuenta con mayor número de demostraciones realizadas a lo largo de los siglos. Alguna de estas atribuida al mismísimo Pitágoras (siglo VI antes de J.C.); aunque el conocimiento de este teorema debe ser muy anterior al nacimiento del célebre matemático griego. Los antiguos chinos ya mostraron algunas en dos libros antiquísimos; el Zhou Bi Suan Jing escrito entre el 500 y 300 antes de J.C. y el Jiu Zhang Suan Shu, escrito en torno al año 250 antes de J.C. Durante la Edad Media se exigía una nueva demostración de este teorema para lograr el título de “Magister matheseos” (maestro matemático) y por ello se conocen según algunos autores más de mil formas diferentes de demostrar este teorema. En cualquier caso, si alguien tiene curiosidad señalo que el matemático estadounidense E.S, Loomis en un libro publicado en 1927 catalogó 367 formas diferentes.
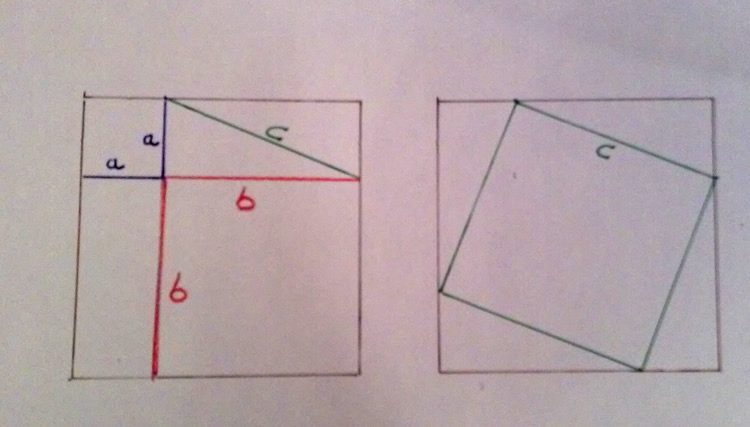
Así las cosas, cabría preguntar al lector: ¿Cómo demostraría Vd. el Teorema de Pitágoras?. Yo algunas veces lo he intentado sin guía alguna y no resulta sencillo. Compruébelo quien quiera. No obstante, haciendo una pequeña “trampa” acudí a la Red y pronto hallé una, (hay muchas) que me parece sencilla de entender. Es la que adjunto a este texto. Creo que no precisa explicación alguna.
Más sencillo resulta demostrar que la suma de los tres ángulos de un triángulo es exactamente (y sin matización alguna) 180º. En el campo de las matemáticas las demostraciones no se hacen a base de experimentos reiterados; si no mediante razonamientos tan evidentes que no precisan nada mas que eso, razonar. Así pues, a quién le cueste demostrar el Teorema de Pitágoras puede probar con el asunto de la suma de los tres ángulos de un triángulo.
Las relaciones entre lados y ángulos en un triángulo rectángulo son esenciales para multitud de aspectos. Dan lugar a una serie de conocimientos que forman parte de la rama de las matemáticas conocida como trigonometría básica, pero que es de enorme utilidad para innumerables de trabajos técnicos (medir fincas, trazar carreteras, construir edificios, medir galerías mineras, …….). Hay que tener en cuenta que las relaciones entre lados y ángulos de un triángulo se mantienen invariables, aunque el tamaño de este cambie. Así sirven para medir la superficie de un papel, un monte o distancias de millones de kilómetros.
LOS OTROS TRIANGULOS
Los triángulos que no tienen un ángulo recto, no se llaman triángulos rectángulos; pero son asimismo de enorme utilidad en muchos campos de la geometría. Tal es así que si conocemos las medidas de lo lados de un triángulo podremos determinar las medidas de sus ángulos. Una superficie por complicada que sea, en general se puede descomponer en triángulos y si conocemos los lados de cada uno de estos podremos saber los ángulos como he señalado y levantar un plano correcto de la superficie. De lo dicho se desprende que se pueden medir ángulos a partir de las medidas de los lados. Esto es muy importante. No todo el mundo dispone de un teodolito o un utensilio similar pero si de una sencilla cinta métrica. Con esta se miden longitudes; como por ejemplo la fachada de un edificio; pero usada adecuadamente sirve también para medir ángulos y en consecuencia hacer planos correctos de una finca por ejemplo. Es mas y por extraño que parezca en ciertos casos usando sólo una sencilla cinta métrica se pueden hacer planos más perfectos y exactos que los realizados usando el teodolito que habitualmente utilizan los topógrafos.
Es una lástima que esta realidad no fuese tenida en cuenta de modo habitual desde hace siglos; pues ello hubiese servido para levantar planos muy correctos con facilidad en muchísimos casos. Una superficie de 4 lados todos diferentes, por ejemplo; puede parecer muy difícil de medir. Sin embargo, si con una sencilla cinta métrica medimos las longitudes de los 4 lados y también eso si de sus dos diagonales podremos hacer por partida doble un plano totalmente correcto de esa finca y lógicamente conocer su extensión.
De lo dicho se deduce que es una lástima que en los documentos que suelen redactarse para definir superficies de 4 lados (fincas muy a menudo); no se tenga ni siquiera hoy día la precaución de señalar las longitudes de los 4 lados y además las de las dos diagonales.
Por último y para terminar citaré un poco de pasada a un tipo de triángulos que son especiales. Se llaman triángulos esféricos y su característica principal entre otras, es que representan superficies, que se forman no sobre un plano; si no sobre una esfera. Son de gran utilidad en el campo de la astronomía o la navegación e incluso y por extraño que parezca también se pueden aplicar en el campo de la geología. Fue precisamente en un libro de geología, en uno de esos apéndices a los que apenas se presta atención; donde hallé por vez primera unas ligeras nociones de esta disciplina matemática, que me serviría para realizar algunos de los trabajos más singulares que he realizado en mi vida; como son los parques solares didácticos.
Rogelio Meléndez Tercero