Incluso personas con unos conocimientos mínimos de geometría saben que el área de un triángulo se halla multiplicando la longitud de su base por su altura y dividiendo el resultado entre dos. Esto es totalmente correcto y así creo que se ha enseñado durante siglos en escuelas y otros centros de enseñanza. Es desde luego una forma de hallar el área del triángulo sencilla y que es muy fácil de justificar, al menos en determinados triángulos, esto es en aquellos en los que la altura es una línea perpendicular a la base del triángulo trazada por el vértice opuesto. Si la altura es la perpendicular trazada a la prolongación de la base ya resulta más complicado demostrar o hacer ver que la fórmula sigue siendo correcta. En cualquier caso yo entiendo que en la práctica, es decir sobre el terreno (no sobre un papel), a veces no es fácil tener la seguridad de que una línea trazada en el suelo es rigurosamente perpendicular a otra. Aquí hay un problema, que no obstante no ha sido suficiente para que la sociedad en general, se decante por la conocida fórmula de “base por altura y partido por dos”.
Sin embargo unos conocimiento digamos medios de matemáticas muestran que hay otros modos de medir el área de un triángulo. Uno de estos es el empleo de la llamada Fórmula de Herón, formula antiquísima que se atribuye al sabio de la Antigüedad llamado Heron de Alejandría, que vivió hace unos 20 siglos. Esto indica que hace por lo menos 2.000 años que se conoce esta fórmula, que sin embargo apenas se utiliza y que en mi opinión tiene muchas ventajas con respecto a la que usa todo el mundo. Lo intentaré justificar a continuación.
Si nos facilitan la base y la altura de un triángulo podremos saber su área, pero no la forma de este triángulo. Sin embargo, si nos facilitan las longitudes de los tres lados de un triángulo es evidente que podemos saber exactamente la forma de ese triángulo, es decir conocer sus ángulos a partir del conocimiento de sus lados que es lo más sencillo de medir en el terreno. La ventaja de la Fórmula de Herón es que permite calcular la superficie de un triángulo sabiendo únicamente las longitudes de sus tres lados. De este modo si sabemos las medidas de los tres lados de un triángulo podremos hacer un plano del mismo rigurosamente exacto. Aquí está la ventaja de esta fórmula ya que en el terreno es muy sencillo medir longitudes pero no lo es tanto medir ángulos. Por ello saber (sobre el terreno) cual es la altura de un triángulo, no es tan simple como parece. En la práctica se mide esta altura intentado hacerlo a ojo, es decir confiando en que la medida se está realizando sobre el terreno de modo perpendicular a la base. Esto sobre una hoja de papel se puede lograr de modo aceptablemente aproximado, pero no en el terreno. Por todo ello la práctica de medir una superficie triangular midiendo sus tres lados y pese a ser poco utilizada por el ciudadano corriente, es la más adecuada.
UN PASO MAS
Aún hay mas que añadir. La mayoría de las fincas o espacios similares por muy extraña e irregular sea su forma, se pueden descomponer en superficies triangulares. Un cuadrilátero, un rombo, un romboide y una infinidad de figuras geométricas se pueden descomponer fácilmente en un conjunto de triángulos adosados unos a otros. Por todo ello si hacemos un croquis a mano alzada ( es decir sin escala) de un terreno irregular y lo descomponemos en triángulos de los que sepamos las longitudes de sus lados, podremos hacer un plano exacto y a escala de ese terreno irregular. En el caso de muchas fincas que son y han sido a menudo polígonos de cuatro lados, el asunto es aún mucho más sencillo. En la práctica esto supone medir ángulos a partir de medidas de longitudes. Las medidas de ángulos a menudo se hacen, (sobre el terreno), utilizando aparatos mas o menos sofisticados y difíciles de manejar, es decir los utilizados por topógrafos o agrimensores. Una cinta métrica o algo similar sin embargo la maneja cualquiera. Aquí esta por tanto el asunto clave.
Si lo normal hubiese sido calcular triángulos utilizando la Fórmula de Herón; sin duda alguna hoy en archivos y bibliotecas tendríamos una información sobre antiguas fincas y similares mucho más rigurosa y exacta de la que tenemos. No obstante la realidad es muy diferente. La Fórmula de Herón es hoy bastante conocida, pero en documentos de hace siglos, se pone de manifiesto a menudo que los conocimientos matemáticos de los escribanos corrientes (lo que hoy son los notarios), eran tan escasos que no les permitían conocer, ni por supuesto manejar esta fórmula matemática. En el célebre Catastro de Ensenada (año 1752); se ponen reiteradamente de manifiesto los escasos conocimientos de matemáticas y geometría de los “técnicos” de la época.
Al analizar viejos archivos con mentalidad matemática, se observa como no se pone en práctica aquello de que “una imagen vale mas que mil palabras”. Los escribanos de hace siglos redactaban extensos y aburridos textos en los que había mucha palabrería y pocos datos concretos. En lo que respecta a las descripciones geométricas en vez de recurrir a la realización de croquis más o menos sencillos, se enredaban con explicaciones en general extensas, ambiguas y confusas. En vez de señalar las unidades de medida empleadas (varas, leguas o lo que fuese) y concretar el número de esas medidas, se utilizaba muy a menudo expresiones ambiguas y confusas. Distancia de un tiro de ballesta o de piedra por ejemplo. Para señalar en que dirección, se hacía una medida también se empleaban expresiones muy imprecisas.
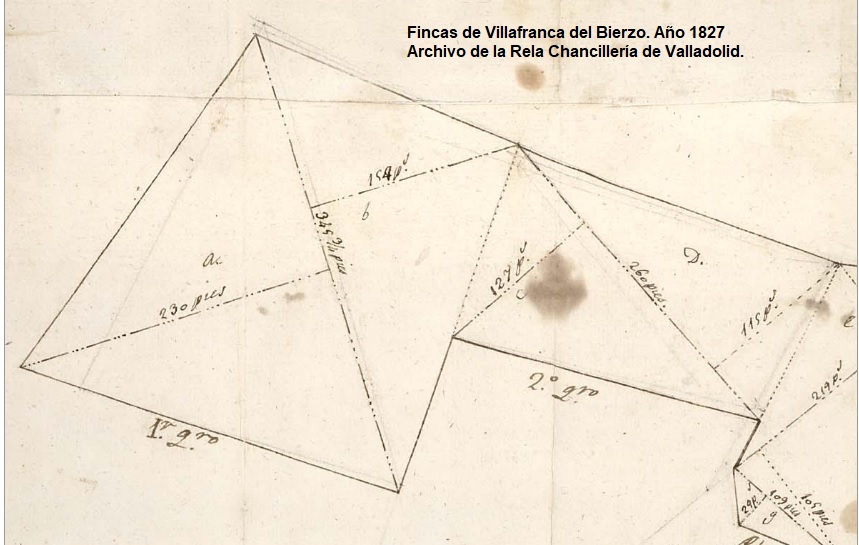
Un ejemplo de esta mala costumbre lo hallé hace escasos días en la Red. Se trata de un documento de la Real Chancillería de Valladolid, en el que aparece un plano de unos terrenos de Villafranca del Bierzo por lo que parece y las medidas de estos. El anónimo autor de ese plano en vez de optar por descomponer ese terreno en triángulos y señalar las medidas de los lados de cada uno de ellos; lo que hizo fue descomponer el terreno en triángulos pero facilitando base y altura de cada triángulo. Es una técnica mas deficiente que la otra. Por ello aunque en el documento aparece un mapa o plano de los terrenos medidos no es posible comprobar si está bien realizado o no. Adjunto imagen.
Rogelio Meléndez Tercero