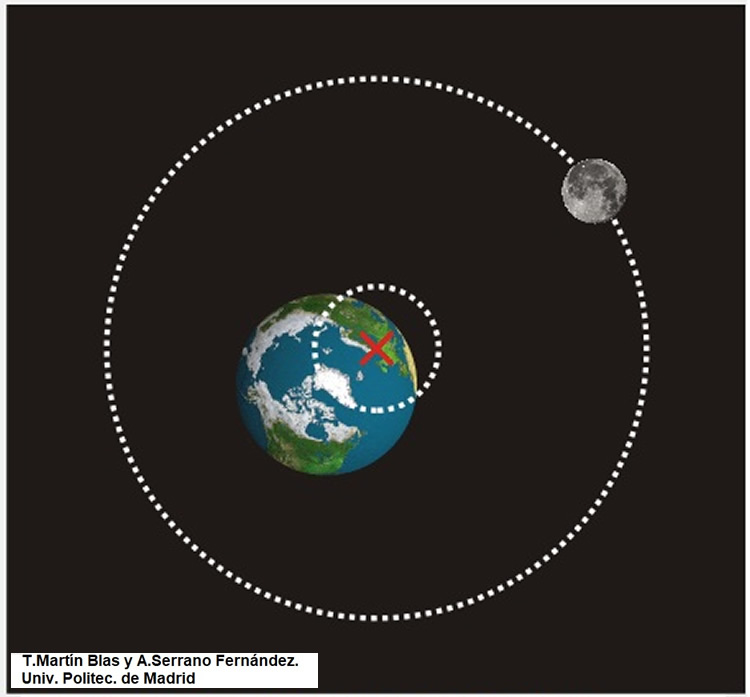
Hay determinadas propiedades o características de la Luna, que son muy conocidas, como su influencia en las mareas. Hay otras “facultades” de La Luna que son muy creídas pero no han sido demostradas de modo indiscutible (influencia de sus fases), sin embargo otras comprobadas o al menos seriamente sospechadas hace siglos aún permanecen un tanto ignoradas, como el hecho de que se aleja de La Tierra. Es muy poco –por supuesto- pero se aleja unos 4 metros cada siglo, es decir unos 4 cm cada año.
¿Porqué hace siglos que sabemos que tiene que ser así?. Pues sencillamente porque los conocimientos de física desde los tiempos de Newton, así lo indican. Vamos a explicarlo.
Cuando un cuerpo está girando sobre si,sea La Tierra o sea un balón de fútbol, las características de este giro se pueden expresar de modo matemático. Para ello hay que tener en cuenta varias características, expresadas siempre con números. Una es la velocidad de rotación. No es lo mismo una velocidad lenta que una rápida. También hay que tener en cuenta la masa del cuerpo. Esto es sencillo de entender. Si una rueda de un automóvil está girando sobre su eje muy lentamente ( a razón por ejemplo de una vuelta cada minuto), la fuerza para frenarla será mucho menor que si está girando a razón de una vuelta cada segundo. También influye la masa. Una rueda de un turismo no es lo mismo que una rueda de las grandes de un tractor. Se necesita mas fuerza para frenar esta última. Por otra parte también es preciso tener en cuenta como se distribuye la masa por una rueda. Si en una parte de esta lleva adosado un peso adicional esto afectará al giro.
Todo esto se expresa de modo matemático y técnico diciendo que la cantidad de movimiento o en concreto el momento cinético de ese cuerpo en rotación es resultado de multiplicar su velocidad de giro por otra magnitud que tiene a su vez en cuenta la masa del cuerpo y su distribución Se le llama momento de inercia. El momento de inercia es el resultado de multiplicar las masas de las infinitas partículas del cuerpo en rotación por sus infinitas distancias al cuadrado al dentro de giro y sumarlo todo. El momento de inercia I es igual al sumatorio de mi ri2, siendo m la masa de esas partículas y r la distancia al eje de giro. El momento cinético es por tanto resultado de multiplicar velocidad de giro x mi y por ri2
Una de las consecuencias de las leyes de Newton es que en un cuerpo que esta girando y si no hay intervención de ninguna fuerza externa el momento cinético debe ser constante. Esto es un tanto complicado de entender, pero quizá ayuda mucho un ejemplo bien conocido. Los patinadores sobre el hielo a veces se ponen a girar sobre si mismos y el modo de hacer que esa velocidad de giro es extender los brazos. Así la distancia media al centro de giro aumenta. Al hacer esto lo que ocurre es que la masa (cuerpo del patinador), se expande y por ello aumenta el momento de inercia, pues lógicamente la masa (cuerpo del patinador sigue siendo la misma). Para que el momento cinético no varíe no queda mas remedio que disminuir la velocidad de giro, que es lo que ocurre en la práctica.
EL CONJUNTO TIERRA-LUNA
La Tierra y La Luna son cuerpos independientes, pero a muchos efectos se comportan como si estuviesen unidos por un eje invisible. En la práctica es como si hubiese una cuerda de la Tierra a la Luna que la sujeta, mientras que la Luna tiende a escaparse (como si en el extremo de una cuerda tenemos un objeto al que hacemos girar).El centro de giro no está en el centro de La Tierra si no a una profundidad de unos 1700 km. Es decir bastante alejado del centro de La Tierra. El sistema Tierra-Luna es pues a ciertos efectos como un único cuerpo en rotación.
Esta rotación sin embargo se sabe que esta siendo frenada por las mareas y otras causas, (que no viene al caso comentar ahora), luego para compensar ese frenado hay que aumentar el momento de inercia y ello sólo se puede hacer alejando la Luna, maniobra esta que sería el equivalente del caso del patinador que extiende sus brazos. El razonamiento es el siguiente: el patinador extiende sus brazos para frenar la rotación de su cuerpo y en el caso del sistema Tierra-Luna, la rotación de la Tierra se ve frenada en consecuencia La Luna debe alejarse para compensar este frenado de la rotación terrestre.
El problema del alejamiento de la Luna se reduce pues a un simple problema de física de secundaria. Pero aclaro que es un problema, respecto al cual no me he puesto a realizar los pertinentes cálculos.
Actualmente es de 0,038 m/ año (3,8 cm al año).Si se mantuviese constante al cabo de 400 millones de años la distancia (media) Tierra-Luna habría aumentado en 400.000.000 x 0,038 = 15.200 Km. y La Tierra entonces giraría mucho mas lenta que ahora tanto que el día duraría 24,2 horas, es decir 24 horas y 12 minutos. Esto último no se de donde lo he sacado. Debería comprobarlo por precaución.
Por tanto desde que se supo que las mareas frenan el giro de la Tierra, ya hubo datos para estudiar el problema . Recientemente las misiones Apolo por ejemplo han confirmado que esto es así. Además el estudio de los eclipses históricos también, lo confirman.
En la Red donde tantas páginas interesantes hay (aunque hay que saber elegir con cuidado), aparece una de la Universidad Politécnica de Madrid, realizada por Teresa Martín Blas y Ana Serrano Fernández que habla del sistema Tierra-Luna y creo que viene muy bien para intentar comprender lo que he tratado de exponer en este artículo, aunque se que es un asunto un tanto complejo para un artículo de divulgación elemental como este. La imagen que adjunto está tomada de esa página de la Universidad Politécnica de Madrid citada.
Rogelio Meléndez Tercero